【壓縮機網】1、緒論
1.1 研究背景及意義
活塞式壓縮機廣泛應用于石油、化工、冶金、天然氣行業,作為一種重要的氣體增壓設備,在一些工藝流程中發揮著關鍵作用,這些設備能否正常運行直接關系到企業的生產能力[1]。在持續安全生產中威脅z*大的是管道振動,而管道振動的z*大誘因就是氣流脈動。由于活塞式壓縮機吸、排氣的非連續性,不可避免使管道內氣體壓力出現周期性的波動,這就是氣流脈動[1,2];活塞式壓縮機管道系統都存在一定程度的氣流脈動,這種脈動的壓力在管道的突變截面、彎頭、盲管、閥門等處產生交變的激振力,進而引發振動,工業現場經常出現劇烈的管道振動導致管路焊接處或法蘭聯接處振斷,造成生產事故。
控制管道振動s*先應準確掌握管道系統的氣流脈動情況,尤其是管道系統中關鍵節點如氣缸連接法蘭、彎頭、閥門等處的壓力脈動幅值。分析氣流脈動的方法主要有兩種,一種是平面波動理論,另一種是一維非定常可壓縮流體流動理論[3]。平面波動理論是研究氣流脈動現象時z*早發展起來的理論,這種方法做了幾個方面的重要假定:壓力脈動值相對管道氣流的平均壓力值很小[4,5];氣體遵守理想氣體的性質;認為管道中氣體流速相對聲速小到可以忽略不計的程度[6]。因此波動理論建立氣體脈動的控制方程時能做線性化處理,z*終得出能求解析解的波動方程。在符合假定的條件下,波動理論能預測出符合實際的壓力脈動幅值。
波動理論作出的假定在數學模型上就決定了它不能完整描述管道內壓力波和非穩態流動耦合的復雜現象。一般認為波動理論對氣體與管道壁面摩擦考慮不足,導致其在脈動幅值較大尤其共振狀態下計算值偏大。此外波動理論在實際求解過程中將整個管道元件中的氣流參數平均值取作氣流參數值進行計算,這就決定了管道內氣流參數值是常數而不是隨實際狀態變化的值,這降低了波動理論的模擬壓力脈動的準確度。
非定常可壓縮流動理論在建立描述管道內氣流脈動現象的控制方程時,沒有忽略非線性因素,綜合考慮了氣體與管道壁面的摩擦問題,實際氣體性質的問題[2]。而且多認為非定常可壓縮流動理論在摩擦問題上處理的更符合實際,因而在脈動幅值較大的情況下計算值比波動理論更符合實測值。但是摩擦阻尼能否顯著抑制脈動幅值還有待進一步驗證,其它影響氣流脈動的因素還有哪些?哪一個因素起了重要作用?如何定量分析它們的影響?這些問題目前研究的還不夠。此外,用非定常方法建立的雙曲型控制方程組需要用數值方法求解,雙曲型方程應用在壓力脈動上會有哪些特性,數值求解的特點、如何獲得較準確的收斂解,這些問題都有待進一步分析。
1.2 氣流脈動研究現狀
氣流脈動的研究是隨壓縮機工業的建立開始的,工程師很早就認識到這種現象對壓縮機管道系統的重要影響,美國西南研究院自20世紀50年代已經展開氣流脈動的理論和實驗研究[7]。1962年,Kinsl和Kfrey[8]z*早提出經典的平面波動理論,至今仍是氣流脈動研究的基礎性理論之一[9],波動理論不考慮管道內氣流流速和氣體實際性質,并忽略非線性因素,z*終得出波動方程,從而用聲波傳播的原理很好的揭示了氣流脈動的機理,對加深認識氣流脈動的本質有重要意義。氣流脈動研究的兩大任務是壓力脈動幅值和氣柱固有頻率的計算,60年代后期有學者開始對壓力脈動幅值計算進行初步探索[10,11]。1970年,日本學者Toru等[12]提出轉移系數法,用結構離散化的思想,將通常復雜的管道系統分割成不同的元件,分別計算。這樣處理的優點是易于實現數字計算機編程,因而得到了廣泛應用,至今仍是脈動計算的主流方法之一。70年代初山田榮[13]、野田桂一郎[14]提出剛度矩陣法,克服了轉移系數法對分支管路處理繁瑣的缺陷。1973年酒井敏之等[15]提出計算復雜管系氣柱固有頻率的轉移矩陣法,仍然借助結構離散化思想,s*先計算每個管道元件的轉移矩陣,再進行總裝配,z*后用計算機求解出各階氣柱固有頻率,這種方法同樣易于編程計算,因而應用非常廣泛。同年,美國的Sodel教授引入經典的亥姆霍茲共鳴器法,開始了壓縮機消聲器研究[16]。以上幾種方法都是基于波動理論發展起來的,而波動理論在阻尼因素上作了線性化處理即認為阻尼與速度成正比,當阻尼超出線性范圍時,計算值比實際值偏大,因此限制了它的應用范圍。后來有研究人員[17]對波動理論進行改進,認為速度的平方決定摩擦力的大小,使波動理論能計算脈動幅值較大的情況,拓展了它的應用范圍。與此同時,不作簡化直接用數值計算手段求解管道內非定常氣流流動控制方程組的方法從70年代初開始,1972年Benson[18]總結了數值模擬方法的一些進展,提出可處理管道邊界的勻熵特征線法。自1974年起,在美國普渡大學歷屆召開的國際壓縮機會議,都會討論氣流脈動項目,大大推動了此項研究。這一年的會議上Singh和Sodel[19]教授共同發表一篇綜述,全面總結了壓力脈動和氣柱固有頻率計算的各種方法,制訂出衰減壓力脈動的評價標準。同年,Elson[20]s*次考慮了氣閥閥片運動和管路壓力波動的相互影響,為精確模擬壓縮機吸、排氣口處壓力脈動情況打下基礎。隨著計算機技術的進步,數值模擬的手段越來越受重視,1976年在普渡大學召開的國際壓縮機會議上,Maclaren[21]等基于一維非定常流動理論,提出了較為完善的數學模型,建立的非線性雙曲型方程組中考慮了氣體與管道壁面的非線性摩擦問題以及管道截面變化的影響,得到與實測波形吻合程度較高的計算結果,驗證了一維非定常可壓縮流動數學模型應用于氣流脈動模擬的可行性;文中對比了特征線法、Lax-Wendroff格式和Leap-Frog格式三種算法的數值計算結果,指出特征線法比后兩種算法計算精度低,而且更容易衰減壓力波的高頻成分,但也指出特征線法是計算邊界節點信息必不可缺的方法,文中還s*次采用非勻熵特征線法計算邊界節點,精度比勻熵特征線法高,該文對數值模擬氣流脈動有巨大的指導意義。此后,以Sodel[22]、Singh[23]為代表的研究人員在前人研究成果的基礎上進一步取得進展,不斷完善氣流脈動的數學模型,將已經取得的成果推廣到結構更復雜的多氣缸大型壓縮機上。隨著理論的不斷成熟,20世紀80年代以后工程界側重控制技術的研究[24-27],并逐步形成了在石化、天然氣工業界廣泛認可的API618標準[28],該標準由美國石油協會聯合會員單位共同制訂,詳細規定了石化與天然氣行業用壓縮機氣流壓力脈動幅值上限和管道振幅允許值,并約定了分析氣流脈動和管道振動的三種方法。此標準的廣泛認可也使壓縮機制造商和用戶越來越重視氣流脈動問題,并積極開發控制技術。美國西南研究院自2007年起,展開以聲學衰減器為突破點的新一代壓力脈動控制技術[29-31],目前已經取得階段性的成果。
國內是西安交通大學的黨錫淇和陳守五教授等人z*早發起氣流脈動的研究。從1974年開始著手,他們借鑒了國外轉移矩陣法、轉移系數法和剛度矩陣法的研究成果,并進一步發展:推導出各種典型管道元件的轉移矩陣[32],在轉移系數法中引入線性摩擦阻尼[33];對一維非定常流動也作了一定研究,推導出等截面管內氣流的非穩態流動控制方程組,用勻熵特征線法處理容器、突變截面、匯流點等元件聯接處,使數值計算得到簡化[34,35];在理論分析的基礎上進行了大量實驗研究[36];在深入理論研究和大量工程實踐的基礎上總結出壓力脈動的控制措施[37,38],他們的研究成果集中體現在一本關于活塞式壓縮機管道氣流脈動與振動的專著上[39]。近年來,國內學者進一步取得進展:2001年,西安交通大學的彭學院教授基于平面波動理論開發出氣流脈動分析軟件,該軟件能夠計算任意復雜管系的氣柱固有頻率及各節點處壓力脈動幅值,為快速分析壓縮機管道系統聲學特性提供了有效工具;2003年,李志博通過大量的實驗驗證了該軟件計算結果的可靠性[40]。
近年來氣流脈動的研究趨勢表現在:以美國西南研究院為代表側重使用納維斯托克斯方程一維流動模型建立描述管道內非穩態氣流流動的控制方程,引入因粘性產生的氣體與管道壁面的摩擦力,改變了以往一維非定常氣流方程中摩擦力靠經驗公式計算的方式[21],方程同樣需要有限元或有限差分的數值方法求解[41],并將這種數值解法定義為時域分析法,將波動理論的解析解法定義為頻域分析法,認為時域法比頻域法作的假設更少,計算結果更符合實際,借助時域法還可以計算出因壓力脈動造成的動態壓力損失,進而幫助設計者改進壓縮機整體性能。因此認為時域法更有價值,投入了大量精力研究它的計算特性,探討提高計算精度的方法。另外也有研究人員[42,43]使用CFD軟件運用三維流動理論模擬管道內氣體的壓力脈動,一般認為緩沖罐、氣液分離器等三維結構特征明顯的元件以及壓縮機吸、排氣口等復雜流道處三維方法的結果更準確,西安交通大學的徐斌[44]用Fluent軟件在大脈動情況下獲得了比一維方法更準確的結果,但也指出一維流動理論在小脈動時精度仍然很高。
以上研究現狀的分析表明,基于一維流動的理論仍是分析壓縮機管道氣流脈動的有效方法,一維非定常流動理論是較為完善的數學模型,隨著計算科學的進步,用數值解法精確模擬管道內流體運動越來越重要,但其計算特性如何;如何準確、可靠的得出結果;怎樣用數值方法定量分析影響氣流脈動的各種因素;摩擦阻尼是否有顯著的影響;如何分析非定常方法和波動理論計算差異。這些問題有待進一步探索,本文將在這些方面進行研究。
1.3 本文所做工作
為了深入研究活塞式壓縮機管道內氣流脈動的機理,探索更加精確的模擬方法,在前人研究的基礎上進一步認識氣流脈動的內在規律,本文擬做以下幾個方面的研究:
1)基于一維非定常可壓縮流動理論建立描述活塞式壓縮機管道內氣流脈動現象的控制方程組,分析差分方程的穩定性條件,在用特征線法建立差分格式的過程中分析穩定性條件的物理意義。
2)編寫一維非定常方法數值計算程序,通過大量的計算分析雙曲型方程數值計算特性和程序的準確度、可靠性。討論影響計算結果準確度的主要因素,尤其是網格長度的影響。
3)搭建專門研究活塞式壓縮機管道內氣流脈動的實驗臺,測量管道不同位置處的壓力脈動值。通過與實驗測量值對比,分析導致計算和實測差異的原因,指出數學模型上可改進之處;定量分析影響壓力脈動波形和幅值的因素,尤其是摩擦阻尼的影響;分析導致波動理論方法和一維非定常方法計算差異的原因;定量評價局部阻力在變截面處抑制氣流脈動的作用。
2、氣流脈動的數學模型及求解
平面波動理論分析氣流脈動時作了理想氣體、等熵流動等假設,并且基本方程忽略了非線性項、氣流平均流速的影響[45]。為了在數學模型上更完整準確的描述脈動現象,本章建立一維非定常氣流流動方程,著重考慮管路中的摩擦、實際氣體性質等問題。
2.1 一維非定常氣流的守恒型方程組
由于實際輸氣管路管徑與管長之比一般非常小,流體在同一截面上的各參數如壓力、密度、速度等可以認為相等[39],所以能夠從一維的角度分析氣流脈動現象。在管道內取相鄰兩個截面形成的微團作為研究對象,推導連續方程、運動方程和能量方程。得出一組描述一維非定常可壓縮氣流運動的偏微分方程。這組方程可以表示成守恒型和非守恒型的形式[46],在空氣動力學數值計算上守恒型方程更受重視[47]。
氣流在管路內作一維流動,則壓力 、速度 、密度 分別為坐標x 和時間t 的函數,即
2.1.1 連續方程
1)通過控制面凈流出控制體的流體質量
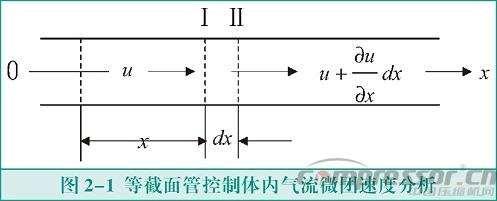
如圖2-1所示取等截面管左側I截面及相鄰右側II截面包圍的空間為控制體,軸向長度取為dx 。在dt時間內由x截面氣流流進的質量為 。由 x+dx 截面氣流流出的質量為:
。由 x+dx 截面氣流流出的質量為:
則 時間內通過I、II控制面凈流出控制體的流體質量為: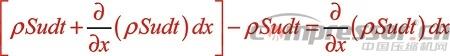
2)控制體內流體質量的變化
在dt 時間內控制體內流體質量的變化為:
3)流體流動的連續方程
根據質量守恒定律,可以得出以下關系式: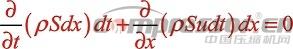
等截面管中橫截面積s是常數,于是可以從上式消去sdxdt ,則得等截面管內流體流動的連續方程: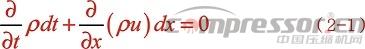
它表示了對于非定常流動,單位時間凈流出控制體的質量等于微元控制體內密度的變化。
2.1.2 動量方程
如圖2-2,在管道內仍取I、II截面內控制體為研究對象,控制體內流體的動量在t瞬時為 ,在dt 時間內的變化量為:
,在dt 時間內的變化量為:

2.1.3 能量方程
能量方程是對流動流體運用能量守恒定律得出的數學表達式。
在等截面管內任取一封閉控制面,其所包圍的空間為控制體。根據能量守恒定律,單位時間控制體內能量的變化量與控制體能量凈流出量之和等于熱交換的能量加上表面力所做的功。所以能量方程的建立要考慮到以下因素[39]:



來源:■文/西安交通大學 王中振
【壓縮機網】1、緒論
1.1 研究背景及意義
活塞式壓縮機廣泛應用于石油、化工、冶金、天然氣行業,作為一種重要的氣體增壓設備,在一些工藝流程中發揮著關鍵作用,這些設備能否正常運行直接關系到企業的生產能力[1]。在持續安全生產中威脅z*大的是管道振動,而管道振動的z*大誘因就是氣流脈動。由于活塞式壓縮機吸、排氣的非連續性,不可避免使管道內氣體壓力出現周期性的波動,這就是氣流脈動[1,2];活塞式壓縮機管道系統都存在一定程度的氣流脈動,這種脈動的壓力在管道的突變截面、彎頭、盲管、閥門等處產生交變的激振力,進而引發振動,工業現場經常出現劇烈的管道振動導致管路焊接處或法蘭聯接處振斷,造成生產事故。
控制管道振動s*先應準確掌握管道系統的氣流脈動情況,尤其是管道系統中關鍵節點如氣缸連接法蘭、彎頭、閥門等處的壓力脈動幅值。分析氣流脈動的方法主要有兩種,一種是平面波動理論,另一種是一維非定常可壓縮流體流動理論[3]。平面波動理論是研究氣流脈動現象時z*早發展起來的理論,這種方法做了幾個方面的重要假定:壓力脈動值相對管道氣流的平均壓力值很小[4,5];氣體遵守理想氣體的性質;認為管道中氣體流速相對聲速小到可以忽略不計的程度[6]。因此波動理論建立氣體脈動的控制方程時能做線性化處理,z*終得出能求解析解的波動方程。在符合假定的條件下,波動理論能預測出符合實際的壓力脈動幅值。
波動理論作出的假定在數學模型上就決定了它不能完整描述管道內壓力波和非穩態流動耦合的復雜現象。一般認為波動理論對氣體與管道壁面摩擦考慮不足,導致其在脈動幅值較大尤其共振狀態下計算值偏大。此外波動理論在實際求解過程中將整個管道元件中的氣流參數平均值取作氣流參數值進行計算,這就決定了管道內氣流參數值是常數而不是隨實際狀態變化的值,這降低了波動理論的模擬壓力脈動的準確度。
非定常可壓縮流動理論在建立描述管道內氣流脈動現象的控制方程時,沒有忽略非線性因素,綜合考慮了氣體與管道壁面的摩擦問題,實際氣體性質的問題[2]。而且多認為非定常可壓縮流動理論在摩擦問題上處理的更符合實際,因而在脈動幅值較大的情況下計算值比波動理論更符合實測值。但是摩擦阻尼能否顯著抑制脈動幅值還有待進一步驗證,其它影響氣流脈動的因素還有哪些?哪一個因素起了重要作用?如何定量分析它們的影響?這些問題目前研究的還不夠。此外,用非定常方法建立的雙曲型控制方程組需要用數值方法求解,雙曲型方程應用在壓力脈動上會有哪些特性,數值求解的特點、如何獲得較準確的收斂解,這些問題都有待進一步分析。
1.2 氣流脈動研究現狀
氣流脈動的研究是隨壓縮機工業的建立開始的,工程師很早就認識到這種現象對壓縮機管道系統的重要影響,美國西南研究院自20世紀50年代已經展開氣流脈動的理論和實驗研究[7]。1962年,Kinsl和Kfrey[8]z*早提出經典的平面波動理論,至今仍是氣流脈動研究的基礎性理論之一[9],波動理論不考慮管道內氣流流速和氣體實際性質,并忽略非線性因素,z*終得出波動方程,從而用聲波傳播的原理很好的揭示了氣流脈動的機理,對加深認識氣流脈動的本質有重要意義。氣流脈動研究的兩大任務是壓力脈動幅值和氣柱固有頻率的計算,60年代后期有學者開始對壓力脈動幅值計算進行初步探索[10,11]。1970年,日本學者Toru等[12]提出轉移系數法,用結構離散化的思想,將通常復雜的管道系統分割成不同的元件,分別計算。這樣處理的優點是易于實現數字計算機編程,因而得到了廣泛應用,至今仍是脈動計算的主流方法之一。70年代初山田榮[13]、野田桂一郎[14]提出剛度矩陣法,克服了轉移系數法對分支管路處理繁瑣的缺陷。1973年酒井敏之等[15]提出計算復雜管系氣柱固有頻率的轉移矩陣法,仍然借助結構離散化思想,s*先計算每個管道元件的轉移矩陣,再進行總裝配,z*后用計算機求解出各階氣柱固有頻率,這種方法同樣易于編程計算,因而應用非常廣泛。同年,美國的Sodel教授引入經典的亥姆霍茲共鳴器法,開始了壓縮機消聲器研究[16]。以上幾種方法都是基于波動理論發展起來的,而波動理論在阻尼因素上作了線性化處理即認為阻尼與速度成正比,當阻尼超出線性范圍時,計算值比實際值偏大,因此限制了它的應用范圍。后來有研究人員[17]對波動理論進行改進,認為速度的平方決定摩擦力的大小,使波動理論能計算脈動幅值較大的情況,拓展了它的應用范圍。與此同時,不作簡化直接用數值計算手段求解管道內非定常氣流流動控制方程組的方法從70年代初開始,1972年Benson[18]總結了數值模擬方法的一些進展,提出可處理管道邊界的勻熵特征線法。自1974年起,在美國普渡大學歷屆召開的國際壓縮機會議,都會討論氣流脈動項目,大大推動了此項研究。這一年的會議上Singh和Sodel[19]教授共同發表一篇綜述,全面總結了壓力脈動和氣柱固有頻率計算的各種方法,制訂出衰減壓力脈動的評價標準。同年,Elson[20]s*次考慮了氣閥閥片運動和管路壓力波動的相互影響,為精確模擬壓縮機吸、排氣口處壓力脈動情況打下基礎。隨著計算機技術的進步,數值模擬的手段越來越受重視,1976年在普渡大學召開的國際壓縮機會議上,Maclaren[21]等基于一維非定常流動理論,提出了較為完善的數學模型,建立的非線性雙曲型方程組中考慮了氣體與管道壁面的非線性摩擦問題以及管道截面變化的影響,得到與實測波形吻合程度較高的計算結果,驗證了一維非定常可壓縮流動數學模型應用于氣流脈動模擬的可行性;文中對比了特征線法、Lax-Wendroff格式和Leap-Frog格式三種算法的數值計算結果,指出特征線法比后兩種算法計算精度低,而且更容易衰減壓力波的高頻成分,但也指出特征線法是計算邊界節點信息必不可缺的方法,文中還s*次采用非勻熵特征線法計算邊界節點,精度比勻熵特征線法高,該文對數值模擬氣流脈動有巨大的指導意義。此后,以Sodel[22]、Singh[23]為代表的研究人員在前人研究成果的基礎上進一步取得進展,不斷完善氣流脈動的數學模型,將已經取得的成果推廣到結構更復雜的多氣缸大型壓縮機上。隨著理論的不斷成熟,20世紀80年代以后工程界側重控制技術的研究[24-27],并逐步形成了在石化、天然氣工業界廣泛認可的API618標準[28],該標準由美國石油協會聯合會員單位共同制訂,詳細規定了石化與天然氣行業用壓縮機氣流壓力脈動幅值上限和管道振幅允許值,并約定了分析氣流脈動和管道振動的三種方法。此標準的廣泛認可也使壓縮機制造商和用戶越來越重視氣流脈動問題,并積極開發控制技術。美國西南研究院自2007年起,展開以聲學衰減器為突破點的新一代壓力脈動控制技術[29-31],目前已經取得階段性的成果。
國內是西安交通大學的黨錫淇和陳守五教授等人z*早發起氣流脈動的研究。從1974年開始著手,他們借鑒了國外轉移矩陣法、轉移系數法和剛度矩陣法的研究成果,并進一步發展:推導出各種典型管道元件的轉移矩陣[32],在轉移系數法中引入線性摩擦阻尼[33];對一維非定常流動也作了一定研究,推導出等截面管內氣流的非穩態流動控制方程組,用勻熵特征線法處理容器、突變截面、匯流點等元件聯接處,使數值計算得到簡化[34,35];在理論分析的基礎上進行了大量實驗研究[36];在深入理論研究和大量工程實踐的基礎上總結出壓力脈動的控制措施[37,38],他們的研究成果集中體現在一本關于活塞式壓縮機管道氣流脈動與振動的專著上[39]。近年來,國內學者進一步取得進展:2001年,西安交通大學的彭學院教授基于平面波動理論開發出氣流脈動分析軟件,該軟件能夠計算任意復雜管系的氣柱固有頻率及各節點處壓力脈動幅值,為快速分析壓縮機管道系統聲學特性提供了有效工具;2003年,李志博通過大量的實驗驗證了該軟件計算結果的可靠性[40]。
近年來氣流脈動的研究趨勢表現在:以美國西南研究院為代表側重使用納維斯托克斯方程一維流動模型建立描述管道內非穩態氣流流動的控制方程,引入因粘性產生的氣體與管道壁面的摩擦力,改變了以往一維非定常氣流方程中摩擦力靠經驗公式計算的方式[21],方程同樣需要有限元或有限差分的數值方法求解[41],并將這種數值解法定義為時域分析法,將波動理論的解析解法定義為頻域分析法,認為時域法比頻域法作的假設更少,計算結果更符合實際,借助時域法還可以計算出因壓力脈動造成的動態壓力損失,進而幫助設計者改進壓縮機整體性能。因此認為時域法更有價值,投入了大量精力研究它的計算特性,探討提高計算精度的方法。另外也有研究人員[42,43]使用CFD軟件運用三維流動理論模擬管道內氣體的壓力脈動,一般認為緩沖罐、氣液分離器等三維結構特征明顯的元件以及壓縮機吸、排氣口等復雜流道處三維方法的結果更準確,西安交通大學的徐斌[44]用Fluent軟件在大脈動情況下獲得了比一維方法更準確的結果,但也指出一維流動理論在小脈動時精度仍然很高。
以上研究現狀的分析表明,基于一維流動的理論仍是分析壓縮機管道氣流脈動的有效方法,一維非定常流動理論是較為完善的數學模型,隨著計算科學的進步,用數值解法精確模擬管道內流體運動越來越重要,但其計算特性如何;如何準確、可靠的得出結果;怎樣用數值方法定量分析影響氣流脈動的各種因素;摩擦阻尼是否有顯著的影響;如何分析非定常方法和波動理論計算差異。這些問題有待進一步探索,本文將在這些方面進行研究。
1.3 本文所做工作
為了深入研究活塞式壓縮機管道內氣流脈動的機理,探索更加精確的模擬方法,在前人研究的基礎上進一步認識氣流脈動的內在規律,本文擬做以下幾個方面的研究:
1)基于一維非定常可壓縮流動理論建立描述活塞式壓縮機管道內氣流脈動現象的控制方程組,分析差分方程的穩定性條件,在用特征線法建立差分格式的過程中分析穩定性條件的物理意義。
2)編寫一維非定常方法數值計算程序,通過大量的計算分析雙曲型方程數值計算特性和程序的準確度、可靠性。討論影響計算結果準確度的主要因素,尤其是網格長度的影響。
3)搭建專門研究活塞式壓縮機管道內氣流脈動的實驗臺,測量管道不同位置處的壓力脈動值。通過與實驗測量值對比,分析導致計算和實測差異的原因,指出數學模型上可改進之處;定量分析影響壓力脈動波形和幅值的因素,尤其是摩擦阻尼的影響;分析導致波動理論方法和一維非定常方法計算差異的原因;定量評價局部阻力在變截面處抑制氣流脈動的作用。
2、氣流脈動的數學模型及求解
平面波動理論分析氣流脈動時作了理想氣體、等熵流動等假設,并且基本方程忽略了非線性項、氣流平均流速的影響[45]。為了在數學模型上更完整準確的描述脈動現象,本章建立一維非定常氣流流動方程,著重考慮管路中的摩擦、實際氣體性質等問題。
2.1 一維非定常氣流的守恒型方程組
由于實際輸氣管路管徑與管長之比一般非常小,流體在同一截面上的各參數如壓力、密度、速度等可以認為相等[39],所以能夠從一維的角度分析氣流脈動現象。在管道內取相鄰兩個截面形成的微團作為研究對象,推導連續方程、運動方程和能量方程。得出一組描述一維非定常可壓縮氣流運動的偏微分方程。這組方程可以表示成守恒型和非守恒型的形式[46],在空氣動力學數值計算上守恒型方程更受重視[47]。
氣流在管路內作一維流動,則壓力 、速度 、密度 分別為坐標x 和時間t 的函數,即
2.1.1 連續方程
1)通過控制面凈流出控制體的流體質量
如圖2-1所示取等截面管左側I截面及相鄰右側II截面包圍的空間為控制體,軸向長度取為dx 。在dt時間內由x截面氣流流進的質量為 。由 x+dx 截面氣流流出的質量為:
。由 x+dx 截面氣流流出的質量為:
則 時間內通過I、II控制面凈流出控制體的流體質量為: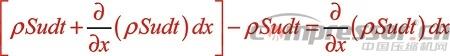
2)控制體內流體質量的變化
在dt 時間內控制體內流體質量的變化為:
3)流體流動的連續方程
根據質量守恒定律,可以得出以下關系式: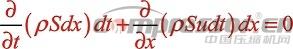
等截面管中橫截面積s是常數,于是可以從上式消去sdxdt ,則得等截面管內流體流動的連續方程: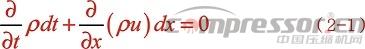
它表示了對于非定常流動,單位時間凈流出控制體的質量等于微元控制體內密度的變化。

2.1.2 動量方程
如圖2-2,在管道內仍取I、II截面內控制體為研究對象,控制體內流體的動量在t瞬時為 ,在dt 時間內的變化量為:
,在dt 時間內的變化量為:

2.1.3 能量方程
能量方程是對流動流體運用能量守恒定律得出的數學表達式。
在等截面管內任取一封閉控制面,其所包圍的空間為控制體。根據能量守恒定律,單位時間控制體內能量的變化量與控制體能量凈流出量之和等于熱交換的能量加上表面力所做的功。所以能量方程的建立要考慮到以下因素[39]:



來源:■文/西安交通大學 王中振




網友評論
條評論
最新評論